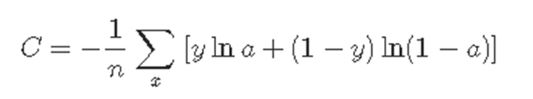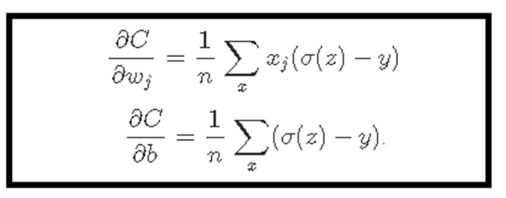refer to http://laonple.blog.me/220548474619
Problem of Neural Network Learning Speed - Learning Slowdown
If the difference between the original value (the result of the training data) and the actual value of network is large, Will the learning really work ?
Generally the method of MSE ( Mean Square Error ) to use the cost function of neural network doesn’t work well unfontunately ‘
Why?
in case that you use the cost function as MSE and Sigmoid as active function, it is because that a problem is assoicated with Sigmoid characteristics
Cause of learning slowdown of neural network – due to the differential nature of sigmoid function
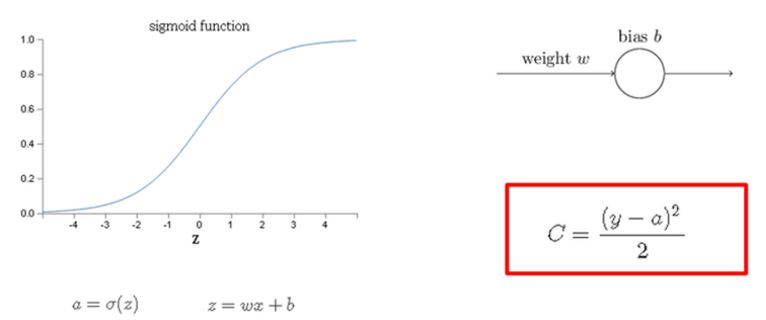
To explain easily let’s guess that we have one neuron, w weight, b bias and active function as sigmoid like as the below picture
When a input is x, the input of neuron is z = wx + b
passing the active function σ(z), the output a comes out.
if the output is y when a input is x ,
the cost function is the red box like as above picture.
Here (y – a) is error , and make the error back-propagate. and then
The larger the error , the faster the learning should be.
As we inspected with back-propagation page,
To update the value of weight and bias the cost function C performs partial-differential for weight and bias.
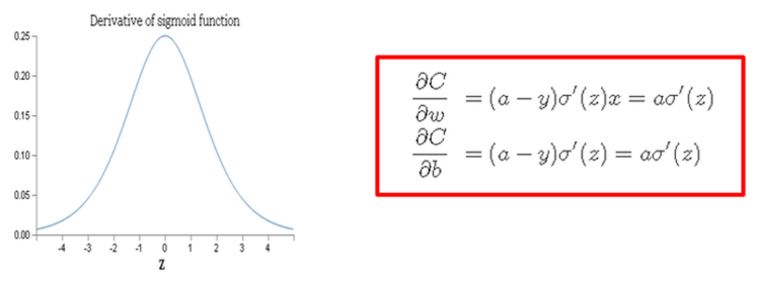
After performing the partial-differential, the result as the below red box comes out.
As you can see from the above equation,
the partial differential value of weight and bias have the multiplication with sigmoid derivative.
Right this is a main curprit.
When we have the derivative for sigmoid function, the result like as the above picture comes out.
That is, z equal to 0 , then get the maximum, and the farther from 0, the smaller to 0 the derivative value goes.
That is, the updated value of weight and bias has a form to multiply the very small value,
and then although (a-y) item is very large, finally the z value would become a very small value, and make the learning speed slowdown.
Cause of learning slowdown of neural network – due to the gradient decent nature
When we see the partial differential equation of C/W,
the value of (a - y ) becomes small, that is, the target value and the real value of network become almost same ,
the value of (a - y ) becomes again close to 0, and finally the updated value of weight and bias become smaller.
finally when goes close to 0, and the learning speed become slowdown.
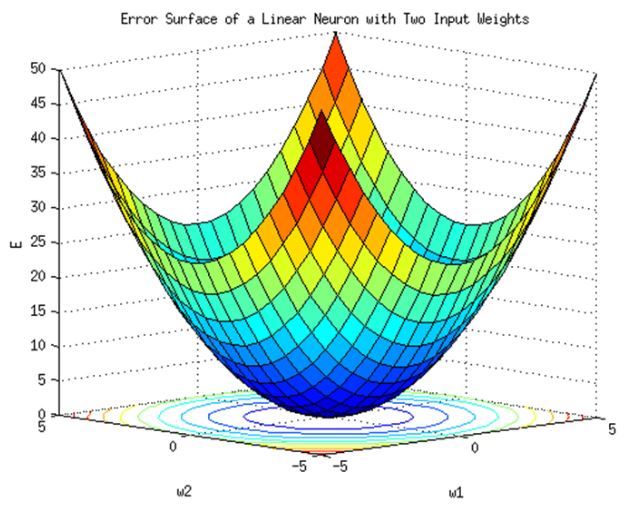
This is due to the structural characteristics of the gradient descent method.
As we saw earlier in “class 8”, the gradient descent method is the result.
When you drop the ball from a high place,
No matter where you start,
The larger the gradient (the larger the gradient), the faster it moves.
Then when it comes to the bottom (ie near the target)
Because there is little slope, the speed at which the ball rolls is slowed down.
Finally when (a - y ) goes close to 0,
the learning speed become slow,
a phenomenon occurs in which the result of learning does not improve so much even if the learning is further performed.
Cross-Entropy
The cross-entropy cost function is defined as follows.
Where y is the expected value,
Assuming that a is a value output from the actual network,
Let n be the number of training data.
Using the sigmoid function as an active function
As we initially expected, we were able to get results that were proportional to the difference between expected and actual output.
As a result, when the learning is performed using the CE cost function,
Because learning progresses much faster
Nowadays, we use CE cost function more than MSE