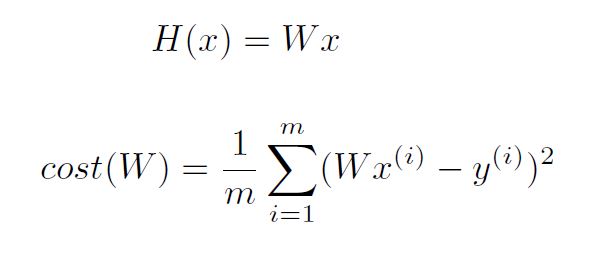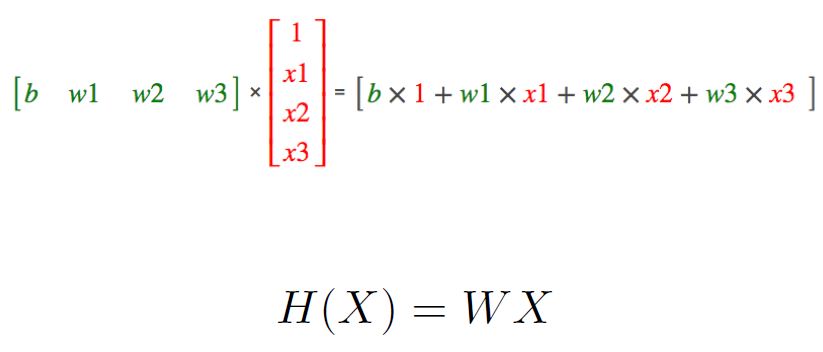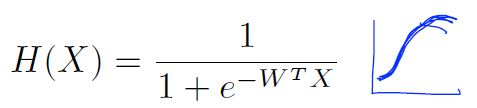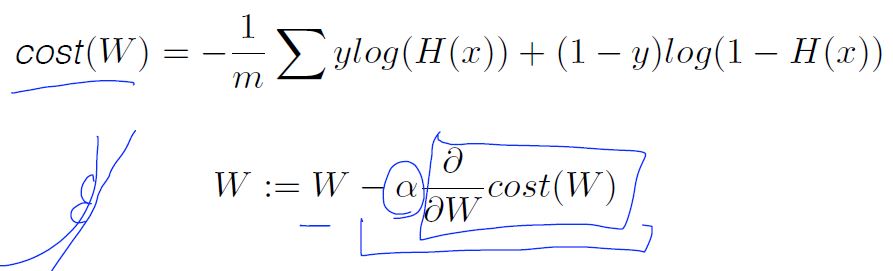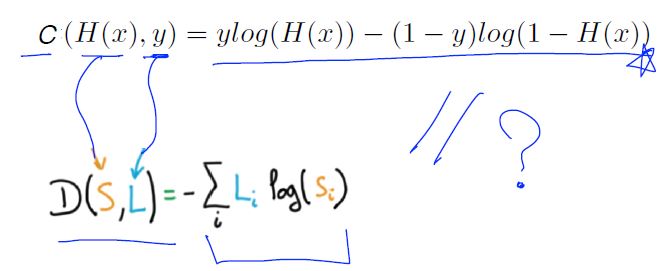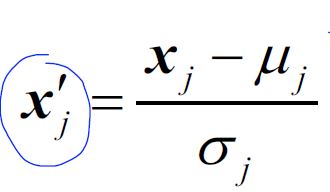Deep Learning summary from http://hunkim.github.io/ml/ (1)

Simplified Hypothesis and Cost

Gradient descent algorithm

• Minimize cost function
• Gradient descent is used many minimization problems
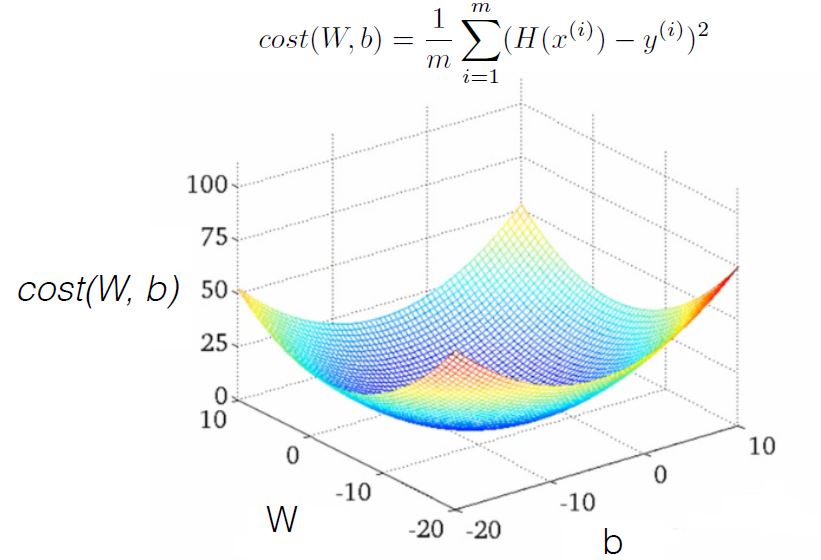
• For a given cost function, cost (W, b), it will find W, b to minimize cost
• It can be applied to more general function: cost (w1, w2, …)

How to work

• Formal definition

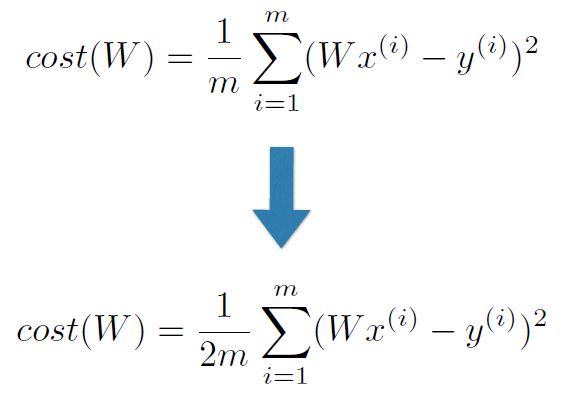
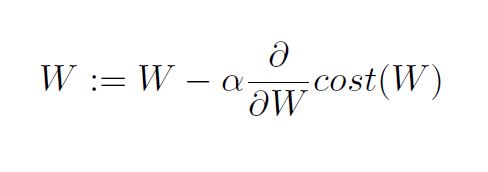
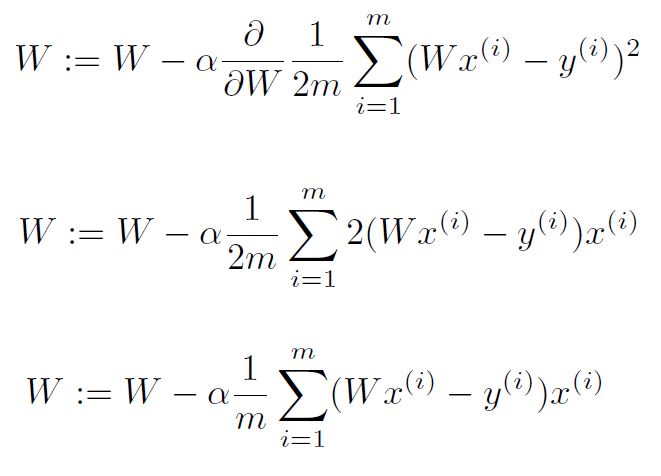
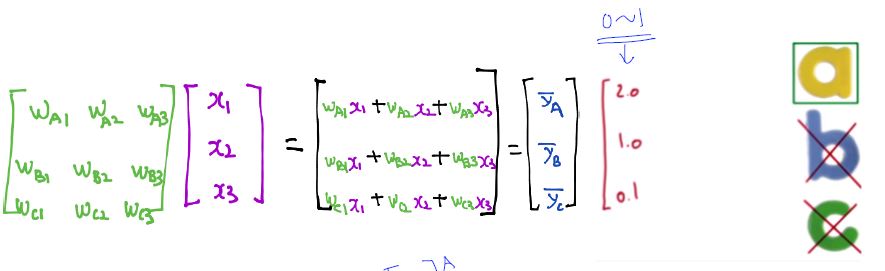
Hypothesis with Matrix

Logistic (regression) classification

Logistic Hypothesis

New cost function for logistic

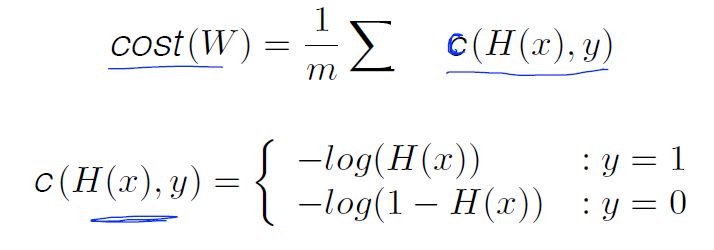
sample code

h = tf.matmul(W, X)
hypothesis = tf.div(1., 1. + tf.exp(-h))

cost = -tf.reduce_mean(Y * tf.log(hypothesis) + (1 - Y) * tf.log(1 - hypothesis))

a = tf.Variable(0.1)  # learning rate, alpha
optimizer = tf.train.GradientDescentOptimizer(a)
train = optimizer.minimize(cost)  # goal is minimize cost

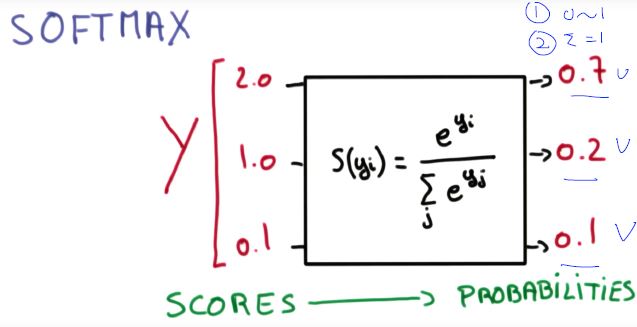
Multinomial classification and Where is sigmoid?

SOFTMAX

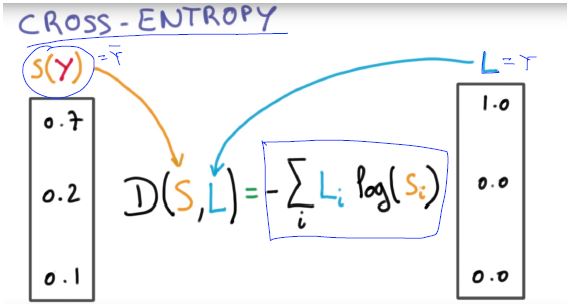
Cross-entropy cost function

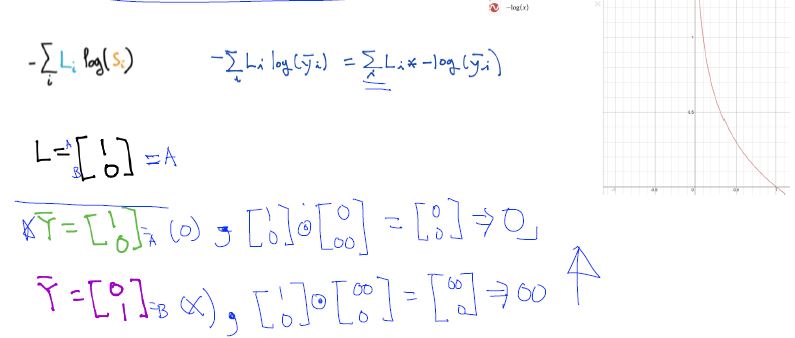
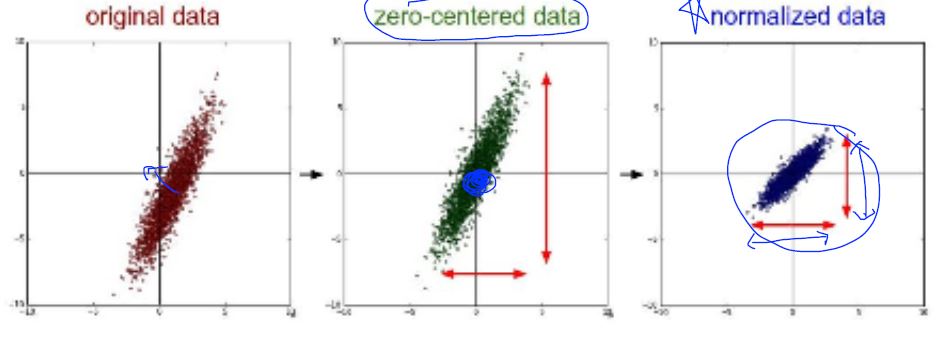
Data (X) preprocessing for gradient descent

standardization

• X_std[:,0] = (X[:,0] - X[:,0].mean()) / X[:,0].std()

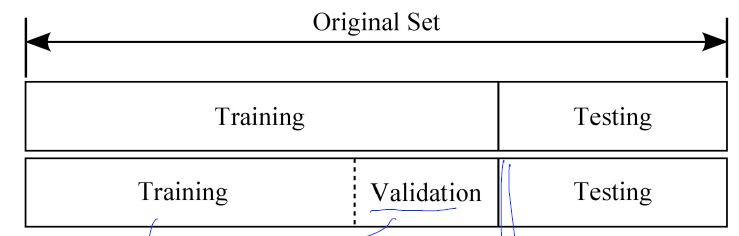
Training, validation and test sets

MINIST Dataset

• train-images-idx3-ubyte.gz : training set images (9912422 bytes)

• train-labels-idx1-ubyte.gz : training set lables (18881 bytes)

• t10k-images-idx3-ubyte.gz : test set images (1648877 bytes)

• t10k-labels-idx1-ubyte.gz : test set lables ( 4542 bytes)

• http://yann.lecun.com/exdb/mnist/